时空变系数(STVC)模型:以探测健康地理现象中的时空非平稳性为例
Original link, in Chinese, from WeChat Official Account “Health and GIS”, 2020.
本微文综合了以下已发表文章的部分内容,对STVC作简单介绍:
Chao Song, Xun Shi & Jinfeng Wang (2020) Spatiotemporally Varying Coefficients (STVC) model: a Bayesian local regression to detect spatial and temporal nonstationarity in variables relationships, Annals of GIS, 26:3, 277-291, DOI: 10.1080/19475683.2020.1782469
Chao Song, Xun Shi, Yanchen Bo, Jinfeng Wang, Yong Wang & Dacang Huang (2019) Exploring Spatiotemporal Nonstationary Effects of Climate Factors on Hand, Foot, and Mouth Disease Using Bayesian Spatiotemporally Varying Coefficients (STVC) Model in Sichuan, China, Science of The Total Environment, 648: 550-60, DOI: 10.1016/j.scitotenv.2018.08.114
Chao Song, Yaode Wang, Xiu Yang, Yili Yang, Zhangying Tang, Xiuli Wang & Jay Pan (2020) Spatial and Temporal Impacts of Socioeconomic and Environmental Factors on Healthcare Resources: A County-Level Bayesian Local Spatiotemporal Regression Modeling Study of Hospital Beds in Southwest China, Int. J. Environ. Res. Public Health, 17, 5890, DOI: 10.3390/ijerph17165890
导读
时空变系数(Spatiotemporally Varying Coefficients,STVC)模型是贝叶斯统计体系下的一类局域时空回归模型,旨在同时探测多个解释变量对目标变量的时空异质性影响,也就是在拟合目标变量与解释变量之间关系时,考虑地理现象中存在的时空非平稳性(spatiotemporal non-stationarity)。在健康地理方面,贝叶斯STVC模型已被用于探测县级水平上中国儿童手足口传染病发生风险与多种气象因子的关联,以及县级水平上中国医疗资源公平性与社会经济和环境因子之间的关联。在这些应用中,STVC模型不仅具备局域时空解释能力,同时表现出较好的模型拟合度与预测效果。
01 背景: 全局与局域空间(时空)回归模型
由于空间自相关(地理学第一定律)和空间异质性(地理学第二定律)的存在,传统的回归模型不适用于处理地理空间数据。空间回归模型能够处理数据中隐含的空间自相关或者空间异质性特征,成为探测地理空间变量之间定量关系的主流方法。
如果两个变量之间的关系(可用回归系数表达)存在空间异质性,也就是在不同的地方有不同的回归系数,统计学将这种变量关系的空间异质性称之为 “空间非平稳性”。按照是否考虑空间非平稳性,空间回归分为两大类:全局空间回归和局域空间回归。全局空间回归,如空间滞后(自回归)、空间误差(自相关)、空间杜宾模型等,通过考虑截距项或残差项的空间自相关效应来提升模型表现。但是,由于不考虑自变量与因变量之间的空间非平稳性,全局空间回归模型有可能出现欠拟合以及解释能力不足等问题,尤其是将这类模型应用于大范围细尺度的地理空间研究对象的时候。
局域空间回归模型考虑了自变量与因变量之间的空间非平稳性。其中,应用最广的两类局域空间回归模型分别是传统频率统计框架下的地理加权回归(Geographically Weighted Regression,GWR)(Brunsdon, Fotheringham, and Charlton 1996; Fotheringham, Charlton, and Brunsdon 1996),以及现代贝叶斯统计框架下的空间变系数(Spatially Varying Coefficients,SVC)模型(Gelfand et al. 2003; Banerjee, Carlin, and Gelfand 2014)。尽管它们输出结果类似,但是在整个建模策略与求解体系上存在本质的不同。相比于基于频率观念的局域空间回归(Frequentist GWR),贝叶斯局域空间回归(Bayesian SVC)的核心优势包括:采用全地图(full map)建模策略(即建立针对全区域的完整和统一的模型),考虑多源先验知识,直接估算参数的不确定性,具有较强的模型可扩展性;而其主要缺点在于复杂度较高,导致计算负担很大,存在对大数据应用的适应性问题。
目前,基于频率观念的GWR模型已经发展了它的时空版,即时空地理加权回归(Graphically and Temporally Weighted Regression,GTWR)(Huang, Wu, and Barry 2010; Fotheringham, Crespo, and Yao 2015),并在不断地改进与发展(Liu et al. 2017; Wu et al. 2019)。而在贝叶斯SVC模型方面,尚无前人正式提出和命名真正的时空版。现在常见的所谓贝叶斯时空模型,仅考虑了截距项的时空异质性,仍然属于全局模型范畴。究其原因,在于贝叶斯局域时空回归建模容易形成过于复杂的表达,特别是在处理地理时空大数据的时候。一方面,复杂表达对推断算法提出更高的要求,导致计算负担过大;更重要的是,全地图(full map)建模策略是一把双刃剑,它在建立统一完整的模型的同时,也面临“Too-Local-To-Model (TLTM)”的问题,即每个局域单元的建模误差会累加,导致整体模型的表现不理想,换句话说,就是过于局域化的时、空、以及时空交互非平稳性假设反而导致无法构建可用的统计模型。前人曾尝试通过大幅度粗化局域尺度来解决该问题,但这样做不仅牺牲了原始空间数据的精细分辨率,还引入了空间分组(聚类、聚合)的额外误差,不是一个理想的解决“过局域”问题的策略。为了解决上述问题,我们提出适用于地理时空大数据建模的贝叶斯时空变系数(STVC)模型 (Song, Shi, et al. 2019; Song, Shi, et al. 2020)。
02 时空变系数(STVC)模型
为了解决“过局域”问题,贝叶斯STVC模型采用了一种时空独立的非平稳假设,即通过分开考虑空间自相关和时间自相关的先验设定,分别估算解释变量后验的局域空间和时间回归系数集合,旨在直接定量刻画变量关系在时间和空间尺度的异质性变化规律。
一个基本的贝叶斯STVC模型体现了贝叶斯层次建模(Bayesian Hierarchical Modeling, BHM)的三个层次思想(公式1-4)。
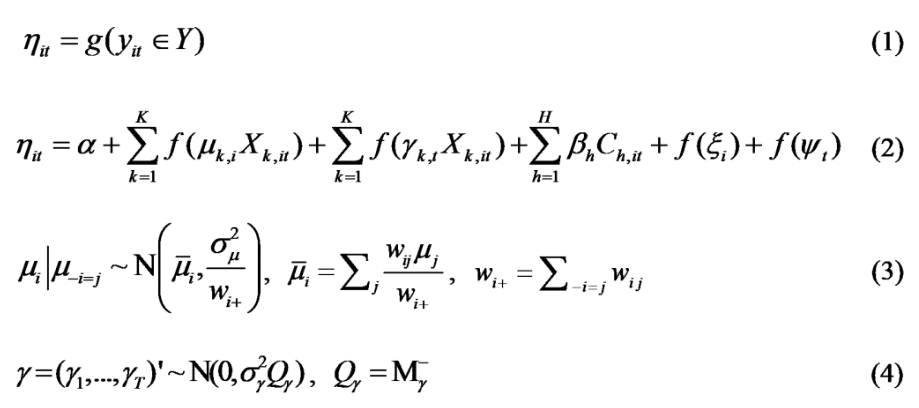

最后,针对地理时空大数据,基于BHM的STVC模型的参数、超参数模型采用了贝叶斯统计的无信息先验设定,体现了数据驱动的建模思想,以适用不同案例的通用建模需求。
除了前文已经总结的贝叶斯局域空间回归建模的优势,贝叶斯STVC模型的特色主要包括:STVC基于时空独立非平稳性的假设,借助全地图BHM建模优势,可直接输出考虑空间自相关(CAR)和时间自相关(RW)效应的局域空间回归系数(SC)与局域时间回归系数(TC)以及它们的可信区间,用于定量探测与全面描述时空非平稳性,且无需时空系数再分析。STVC的局域时空回归建模思想不仅大幅降低了模型复杂度,并由此减小了贝叶斯推断的计算负担,提高了其应用于地理时空大数据时的计算可行性和算法可塑性,同时增强了它对复杂时空变量关系的直观解释能力,方便用户挖掘现象背后的时空作用机理与响应机制。此外,STVC是一类可同时探测解释变量的全局平稳性和局域时空非平稳性的混合模型。
与基于频率统计观念的GTWR相比,首先,STVC是一个真正完整的全地图(full map)模型,这与空间贝叶斯SVC与GWR的区别是类似的。STVC考虑先验知识和不确定性,对解释变量共线性以及目标变量缺失值有较强的灵活适应性,避免了GTWR对带宽设定的过度敏感性,并支持空间邻接概念化关系以避免局域建模的样本量不足的问题。其次, GTWR采用时空交互非平稳假设,而STVC则是基于时空独立非平稳假设,以解决贝叶斯统计框架下局域时空回归特有的“过局域(TLTM)”问题,并能够提高模型在应用于地理时空大数据时的算法可行性。最后,正是由于STVC是基于时空独立非平稳假设,它能够分开输出空间非平稳性SC地图和时间非平稳性TC曲线,方便用户直接分析时空异质性变化规律;而GTWR输出的则是时空耦合的系数集合,一般仍需要再分析,来发现潜在的规律。贝叶斯STVC与频率统计GTWR的对比是一个值得后续研究的话题。但是,前人研究发现,在贝叶斯和频率统计两种体系下,相同的带宽设定是无法转化的,造成了直接对比的困难(Wolf, Oshan, and Fotheringham 2018)。此外,只有应用于一个相对小型的时空数据集时,两者才能服从相同的时空交互非平稳假设,支持相对公平的对比评价。
03 在健康地理领域的应用案例
3.1 探测手足口病发生风险与典型气象因子的时空关联
试验数据包括四川省2009-2011年36个月的县市空间尺度手足口病数据,以及相关的6种气象因子和14种社会经济因子。图1展示了本文的新版图形摘要(Song, Shi, et al. 2019)。
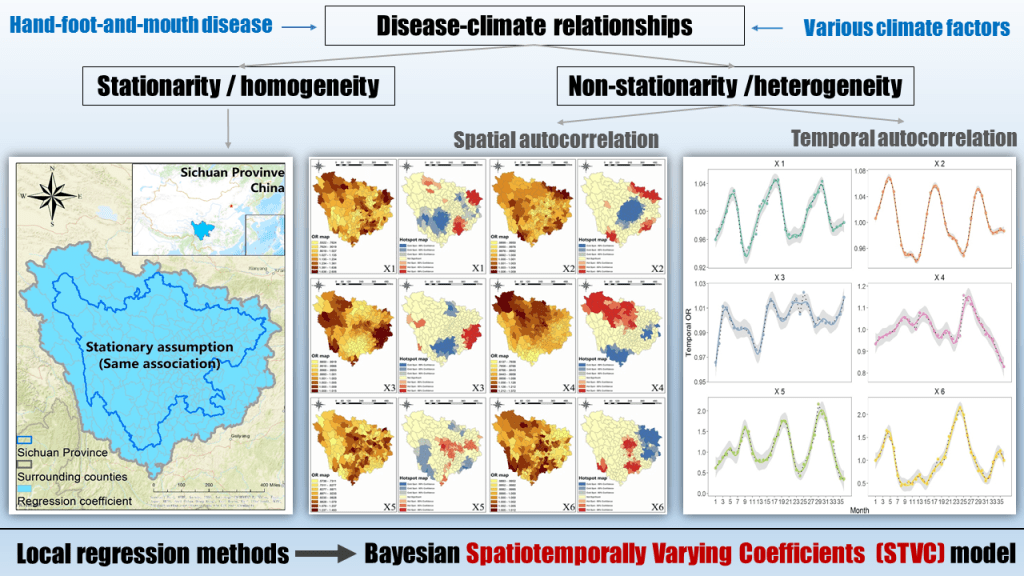
▲ 图1 论文图形摘要(新版):基于传统平稳性假设的全局回归系数制图(左图); 基于贝叶斯STVC模型拟合的考虑空间自相关随机效应的空间系数(Space-Coefficients, SC)地图(中图);基于Bayesian STVC模型拟合的考虑时间自相关随机效应的时间系数(Time-Coefficients, TC)趋势图(右图)。
交叉验证(cross validation)显示STVC的预测正确率(81.98%),优于传统的多变量(68.27%),时间(72.34%),空间(75.99%)和时空(77.60%)生态回归模型。本研究中,以logistic分布为似然先验的STVC模型能够将传统流行病风险评价指标,比值比(Odds Ratio, OR)降尺度为局域ORs(local ORs),用于表征在时间和空间的局域尺度上疾病与气象因素风险关联的异质性变化特征,也就是这种关联会随着时间和地点的不同而不同。针对“疾病自身”以及“疾病与气象关联”这两大类风险,我们探测到了明显的季节效应和显著的空间集聚性。局域时间尺度上,研究发现环境温度,相对湿度和风速的时间非平稳性(temporal ORs)与疾病变化具有相似的季节效应,是典型的时间风险因子。局域空间尺度上,空间非平稳性地图(spatial ORs)清晰展示了哪种气象因素在哪里的影响效应最大,以及显著的风险影响集聚区在哪里,以期因地制宜地的指导制定手足口病地区风险防控政策。
3.2 探测中国东北地区医疗资源与社会经济的时空关联
这一实例研究利用STVC模型,探测了中国东北地区医疗资源与不同典型社会经济因子的时空非平稳性关联,图形摘要如图2所示。研究发现,在全局和局域时空尺度上,个人经济水平、政府投入和区域经济共同影响着中国东北地区的医疗产业发展。在时间维度上,基于具体时间段(局域时间非平稳)的分析发现,从2002至2011十年期间,政府的宏观调控作用越来越强,逐渐成为主导因子。在空间维度上,根据模型结果,绘制了东北地区县级尺度社会经济因子对医疗资源的贡献影响地图集(局域空间非平稳),旨在为决策者提供医疗资源精准配置与优化的政策建议(Song, Shi, et al. 2020)。
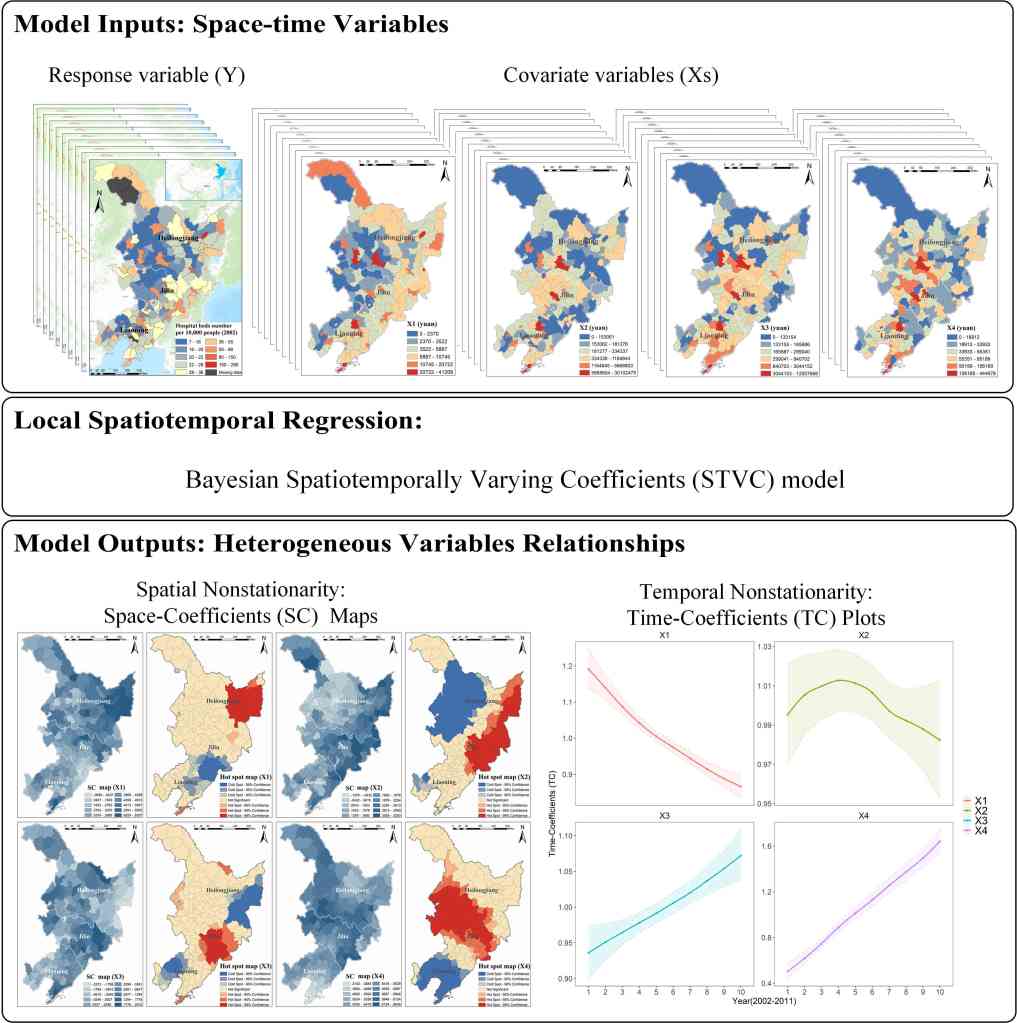
▲ 图2 论文图形摘要:基于贝叶斯STVC模型探测中国东北县级医疗资源与四种典型社会经济因子(X1城乡居民人均储蓄余额,X2人均金融机构贷款余额,X3人均国内生产总值GDP,X4人均第一产业产值)之间的时空非平稳性。
3.3 评估环境和社会经济因素对医院床位数不公平性的时空影响
研究针对医疗资源相对缺乏的中国西南地区,选取20类社会经济因子和12类环境因子作为潜在影响因素,利用STVC模型探测了环境和社会经济因子与县级医院床位资源不公平分布的时空关联(如图3和图4所示),并根据模型结果生成了中国西南地区人均医院床位数公平性地图集(图5),旨在帮助制定中国西南地区公共卫生政策,促进医疗设施公平性与可持续发展。该研究的政策意义在于:大尺度(省级)政策的应侧重于关注全局影响因素(全局回归),而小尺度(县市)的措施则应考虑时空非平稳性从当地最重要的局部影响因素入手(局域时空回归),真正精准实现政策制定与落地(Song, Wang et al. 2020)。
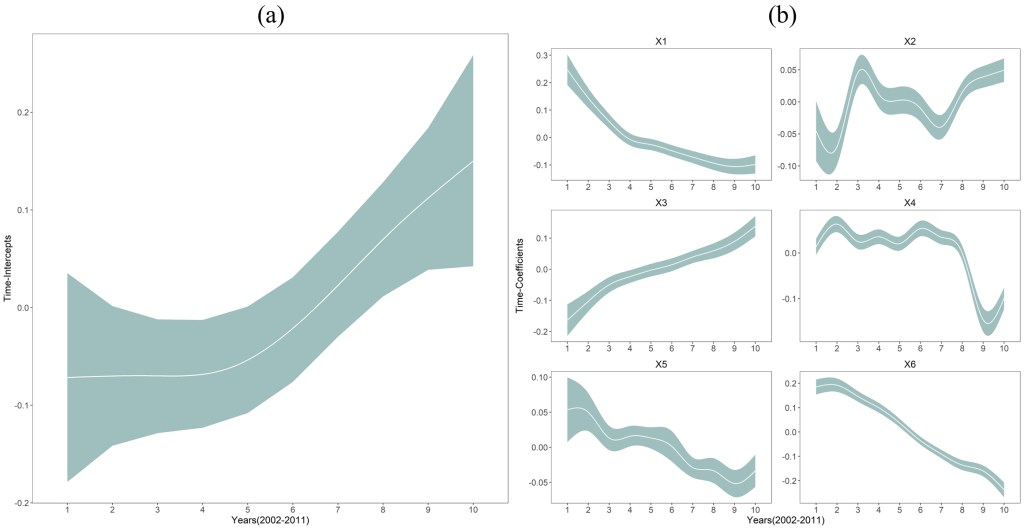
▲ 图3 (a)时间截距(TI)曲线(95%可信区间):研究区十年期间医院床位资源的整体发展趋势; (b) 时间系数(TC)曲线(95%可信区间):环境、社会经济解释因子与医院床位资源的时间异质性关联效应。
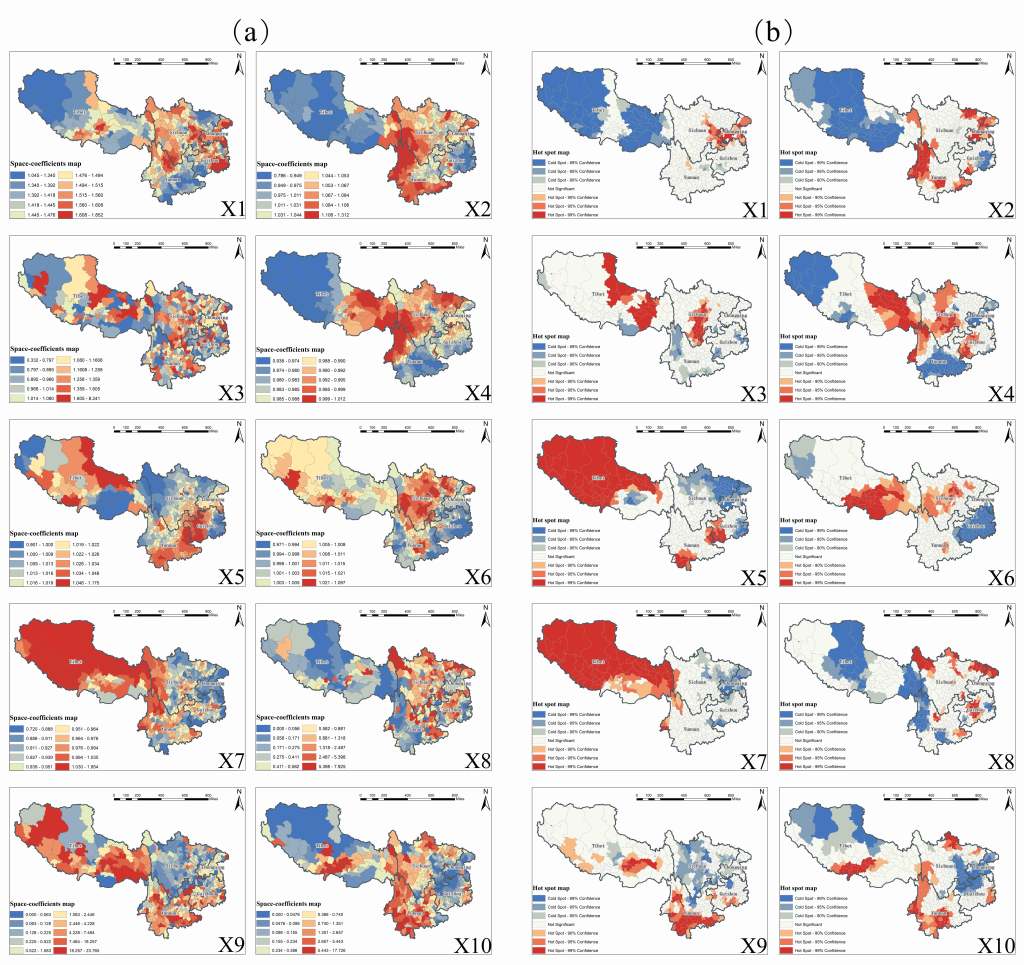
▲ 图4 (a)空间系数(SC)地图集:环境、社会经济解释因子与医院床位资源的空间异质性关联效应; (b)空间系数热点地图集:解释因子空间非平稳性的集聚性效应。
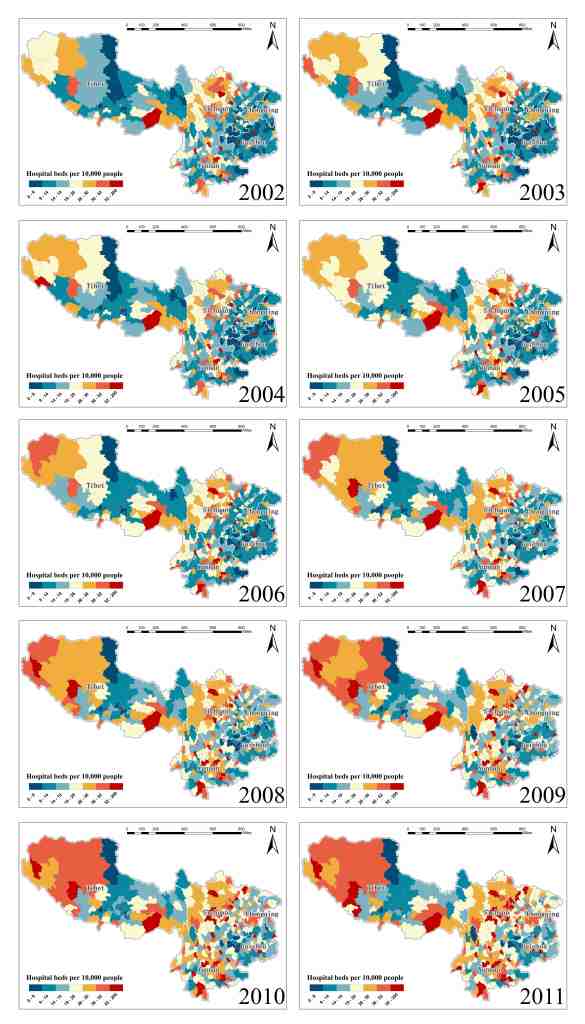
▲ 图5 基于贝叶斯STVC模型预测的中国西南地区医院床位资源完整时空非公平性分布地图集。
值得一提的是,本实例研究中原始目标变量(医院床位资源)数据存在缺失值,但是STVC模型依然能够生成连续完整的空间非平稳SC地图和时间非平稳TC曲线,说明该方法对存在缺失值的情形具有较强的适应性。此外,本研究采用的“解释驱动型”STVC是一个不考虑时空截距项的简化模型,但其各方面评价表现依然优于其他的主流回归模型,表明了贝叶斯STVC模型在以解释与预测兼顾为目标研究中的应用潜力。
3.5 STVCapp:STVC建模时空可视化Web平台
我们最近开发了STVCapp工具的时空可视化模块,结合健康地理学的实际案例展示贝叶斯STVC的建模过程,用户使用浏览器即可使用。图6展示了平板手机端的载入界面。
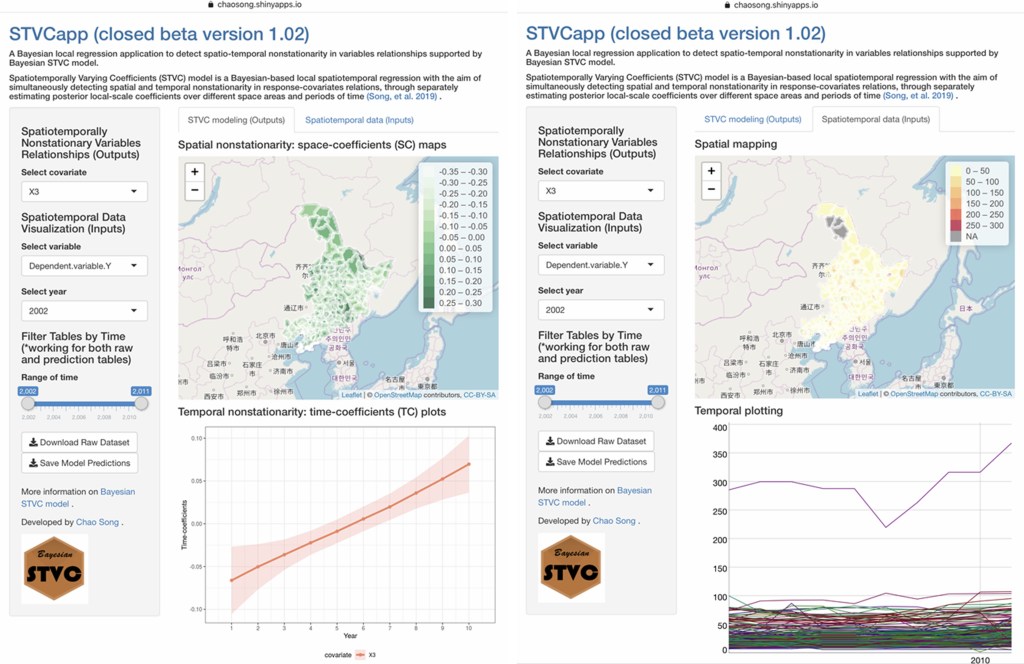
▲ 图6 STVCapp:基于贝叶斯STVC模型的局域时空回归建模可视化展示web工具 (网址:https://chaosong.shinyapps.io/stvcapp/,注:受限于国外云服务器,国内网络使用体验可能较差)
04 结语与展望
贝叶斯STVC模型能够有效处理并探测时空非平稳性,是进行局域时空影响因素分析和时空预测的新工具,在健康地理和其他地学领域有更广泛的潜在应用价值。
未来,我们将对贝叶斯STVC模型不断改进优化,包括纳入更多重要的地理空间特征,如空间分异性(SSH)(Wang, Zhang, and Fu 2016)、空间重复性(地理学第三定律)(Zhu et al. 2018)等,以及提高算法潜力和扩展能力,使贝叶斯STVC模型更加适应于基于地理时空大数据的复杂应用场景。
参考文献
详见已发表的期刊原文。
文案 | 宋 超 编辑 | 郭珮珺 责任编辑 | 姚申君 审核 | 施 迅
欢迎投稿:healthgis@126.com
